最优化-有约束最优化方法

最速下降法

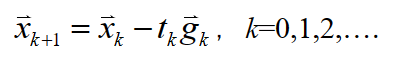
t为步长 $x_k$是迭代出的第k个向量 $g_k$是梯度

---

性质：

锯齿现象：相邻两次迭代点的梯度正交($g_k,g_{k+1}$)

线性收敛，不具有二次终止性，一般要无限步迭代（某些特殊初始点可以有限步终止）

---

当原函数为正定二次函数时，t有显式计算公式

（其他无约束最优化方法的步长均可使用该公式）：

$Q\equiv G$

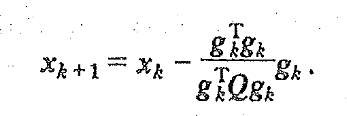
非二次正定函数时，只能使用代入函数，对t求导使其导数为零的方式寻找最优步长

---

原函数二阶导矩阵，即$G_k$ Hession矩阵为正定时，最终的结果是严格局部极小点

Newton法

---

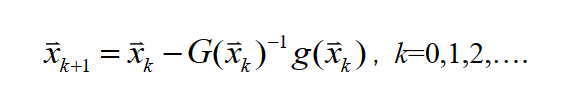
性质：

二次终止性 二阶收敛

对于正定二次函数，迭代一步得到极小点

非正定函数，一般不会有限步终止，通常使用修正Newton法

---

修正Newton法

当$G$奇异时(不存在$G^{-1}$) 使用直线搜索法,即$x_{k+1} = ls(x_k,p_k)$ 也就是$x_{k+1} = x_k + t*p_k$,记该式为公式1 ($p_k默认为-G_k^{-1}*\vec{g_k}$)

当$G$非奇异时,沿用Newton迭代公式 $X_{k+1} = X_k + p_k$ , $p_k=-G_k^{-1}*\vec{g_k}$

1. 若$x_{k+1}<x_{k}$ 迭代有效

2. 若$x_{k+1}\geq x_{k}$ 迭代无效,使用以下规则:

   2.1 当 $|g_k^Tp_k| \leq \phi$ ($\phi$是一个接近于0的整数) 时 ,说明g与p几乎垂直,即p是不利的方向,改取 p为$-g$,按公式1运算(此时退化为最速下降法)

   2.2 当 $g_k^Tp_k < -\phi$时,p为下降方向,按公式1计算

   2.3 当 $g_k^Tp_k > \phi$时,p为上升方向,改取p为-p,按公式1计算

共轭方向法

共轭方向法具有二次终止性.
对于n元正定二次函数，共轭方向法至多迭代 n 次即可求到极小点
对于非正定二次函数，共轭方向法一般不会有限步迭代终止

---

F-R共轭梯度法

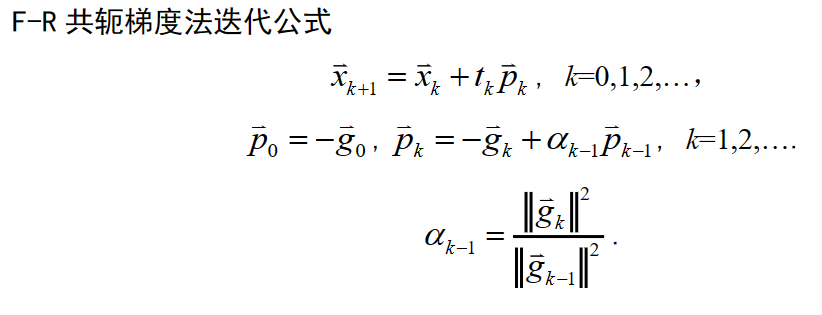
共轭梯度法是共躯方向法，是下降算法，超线性收敛

矩阵的二范数（Frobenius 范数）是矩阵元素平方和的平方根

---

DFP法

DFP 法是共扼方向法，是下降算法，超线性收敛.

步长加速法

略

最小二乘法

即最小化线性回归模型($y=\beta_0+\beta_1x+\phi$)的残差平方和

Minimize $\sum^n_{i=1} (y_i-(\beta_0+\beta_1x_i))^2$

解$A^TA\vec x=A^T\vec b$ 得最小二乘解 $\vec x = {A^TA}^{-1}A^T\vec b$ ,同时也是回归方程的解

线性方程组的解指带入最小二乘解的值$s(\vec x)= f_1^2(\vec x)+f_2^2(\vec x)+\cdots+f_m^2(\vec x)$

s为零则有解,s不为零无解