树状数组/线段树/差分知识点

树状数组

1.应用范围

​ 区别于普通数组的O1更改和On求区间和，前缀和数组的O1求区间和和On更改 树状数组拥有更加均衡的Ologn的求和与更改速度，适合两种情况均大量出现的情景，同时，树状数组可以处理区间更改和查询问题。

​ 树状数组解决的问题线段树都能解决，然而树状数组复杂程度低于线段树。

2.原理介绍

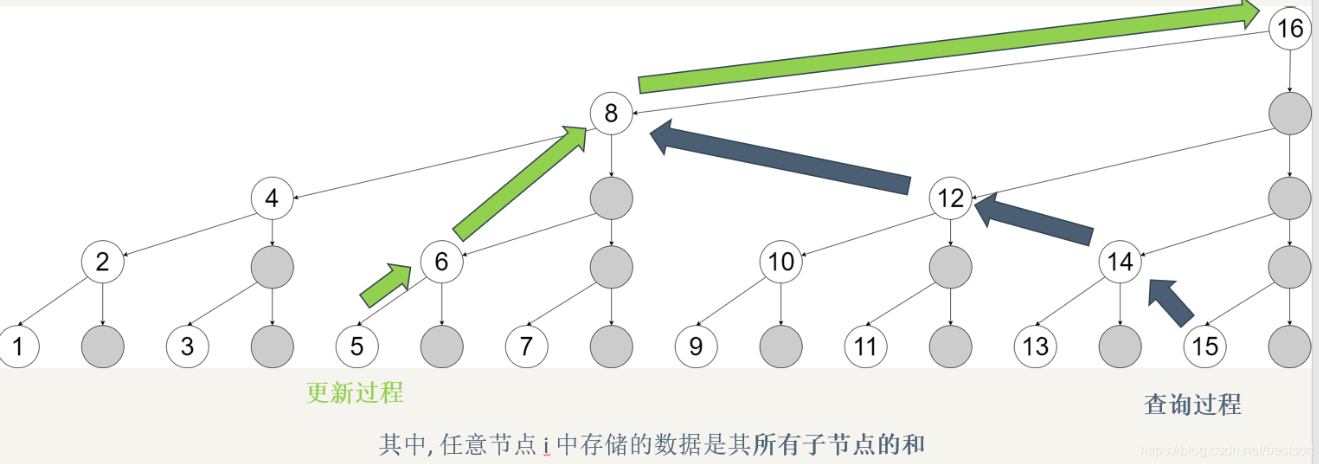
下面是二进制版本，能看到

更新过程是每次加了个二进制的低位1(101+1 ->110, 110 + 10 -> 1000, 1000 + 1000 -> 10000)

查询过程每次就是去掉了二进制中的低位1(1111 - 1 -> 1110, 1110 - 10 -> 1100, 1100 - 100 -> 1000)

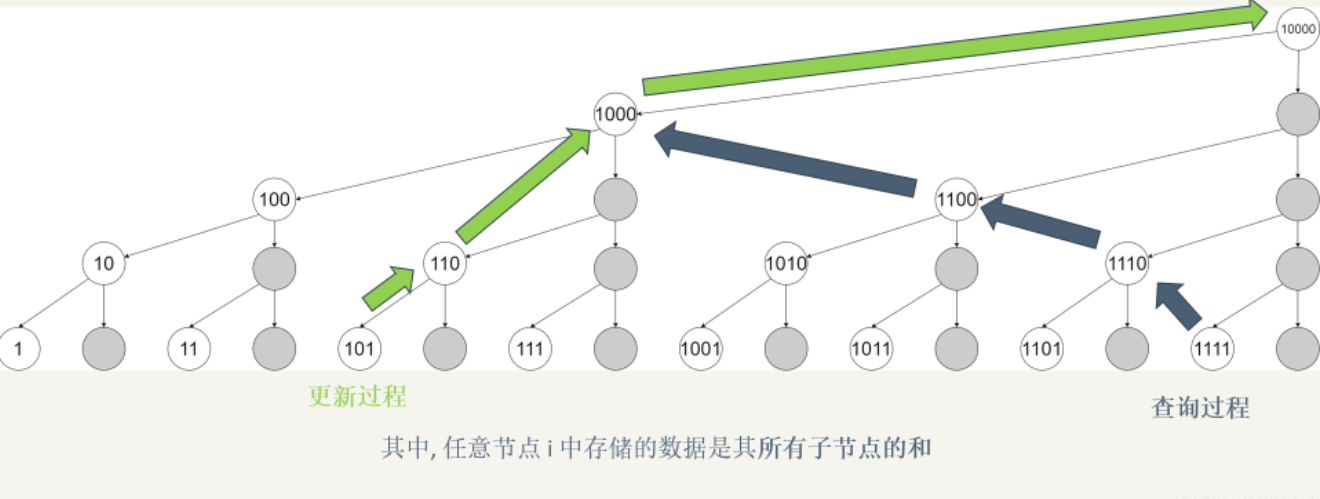
3.低位1的获取

int lowbit(x){return x&(-x);}

4.单点更新

记原始数组为A，树状数组为C

则如果我们要更改A[1]，有以下需要进行同步更新

1(001) C[1]+=A[1]

lowbit(1)=001 1+lowbit(1)=2(010) C[2]+=A[1]

lowbit(2)=010 2+lowbit(2)=4(100) C[4]+=A[1]

lowbit(4)=100 4+lowbit(4)=8(1000) C[8]+=A[1]

换成代码就是:

void update(int x,int y,int n){
    for(int i=x;i<=n;i+=lowbit(i))    //x为更新的位置,y为相较于原值新值增加的值,n为数组最大值
        c[i] += y;
}

5.区间查询

区间查询:
举个例子 i=5

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

可以推出: sum(i = 5) ==> C[4]+C[5];

序号写为二进制: sum(101)=C[(100)]+C[(101)];

第一次101,减去最低位的1就是100;

单点更新的逆操作

代码如下:

int getsum(int x){
    int ans = 0;
    for(int i=x;i;i-=lowbit(i))
        ans += c[i];
    return ans;
    }

6.例题

307. 区域和检索 - 数组可修改

class NumArray {
private:
    vector<int> tree;
    vector<int> &nums;

    int lowBit(int x) {
        return x & -x;
    }

    void add(int index, int val) {
        while (index < tree.size()) {
            tree[index] += val;
            index += lowBit(index);
        }
    }

    int prefixSum(int index) {
        int sum = 0;
        while (index > 0) {
            sum += tree[index];
            index -= lowBit(index);
        }
        return sum;
    }

public:
    NumArray(vector<int>& nums) : tree(nums.size() + 1), nums(nums) {
        for (int i = 0; i < nums.size(); i++) {
            add(i + 1, nums[i]);
        }
    }

    void update(int index, int val) {
        add(index + 1, val - nums[index]);
        nums[index] = val;
    }

    int sumRange(int left, int right) {
        return prefixSum(right + 1) - prefixSum(left);
    }
};

7.高级应用

区间更新+单点求和

把x-y区间内的所有值全部加上k或者减去k，查询某个点的值

通过“差分”（就是记录数组中每个元素与前一个元素的差），可以把这个问题转化为问题1。

//此时的树状数组是差分形式，即先将原数组差分化，再对该数组树状化
void add(int p, int x){ //这个函数用来在树状数组中直接修改
    while(p <= n) sum[p] += x, p += p & -p;
}
void range_add(int l, int r, int x){ //给区间[l, r]加上x
    add(l, x), add(r + 1, -x);
}
int ask(int p){ //单点查询
    int res = 0;
    while(p) res += sum[p], p -= p & -p;
    return res;
}

区间更新+区间求和

把x-y区间内的所有值全部加上k或者减去k，查询某个区间的和

基于问题2的“差分”思路，考虑一下如何在问题2构建的树状数组中求前缀和：

查询
位置p的前缀和即：(p+1)*[sum1数组中p的前缀和 - sum2数组中p的前缀和]。

区间[l, r]的和即：位置r的前缀和 - 位置l的前缀和。

修改
对于sum1数组的修改同问题2中对d数组的修改。

对于sum2数组的修改也类似，我们给 sum2[l] 加上 l * x，给 sum2[r + 1] 减去 (r + 1) * x。

void add(ll p, ll x){
    for(int i = p; i <= n; i += i & -i)
        sum1[i] += x, sum2[i] += x * p;
}
void range_add(ll l, ll r, ll x){
    add(l, x), add(r + 1, -x);
}
ll ask(ll p){
    ll res = 0;
    for(int i = p; i; i -= i & -i)
        res += (p + 1) * sum1[i] - sum2[i];
    return res;
}
ll range_ask(ll l, ll r){
    return ask(r) - ask(l - 1);
}

树状数组解决RMQ问题

//树状范围：【x-lowbit(x)+1,x】
int a[N],c[N]//原数组和树状数组
int lowbit(int x)
    return x&-x;
void ST(int x){//将x更改树状范围内的最大值
	c[x]=a[x];
    for(int i=1;i<lowbit(x);i<<=1){//隐含的递归逻辑 x-i必然是处理过的c
		c[x]=max(c[x],c[x-i]);
    }
}
int query(int l,int r){
	int maxv=INT_MIN;
    while(l<=r){
		maxv=max(maxv,a[r])//如果区间范围小于r的树状范围，只处理r下标这一个位置，r--，以期望r的树状范围小于区间
         r--;
        for(;l<=r-lowbit(r);r-=lowbit(r))//区间范围大于r的树状范围 获得树状范围最大值并缩短区间
            maxv=max(maxv,c[r]);
    }
    return maxv;
}

8.模板题

区间修改、单点查询模板题目：https://www.luogu.org/problem/show?pid=3368

区间修改、区间查询模板题目：https://vjudge.net/problem/POJ-3468

线段树

1.建树

struct SegmentTree{
    int l,r;
    int val;
}tr[4*N];
//更新函数，这里是实现最大值 ，同理可以变成，最小值，区间和等
void pushup(int u)
{
    tr[u].val=max(tr[u*2].val,tr[u*2+1].val);
}
//u为当前需要建立的结点，l为当前需要建立区间的左端点，r则为右端点
void build(int u,int l,int r)//递归方式建树 build(1,1,n);
{
    tr[u].l=l;
    tr[u].r=r;
    //左端点等于右端点，即为叶子节点，直接赋值即可
    if(l==r)
    {
        tr[u].val=a[l];	//此时l==r，也可以写成tr[u].val=a[r];
        return;		//回溯
    }
    int mid=(l+r)/2; //mid则为中间点，左儿子的结点区间为[l,mid],右儿子的结点区间为[mid+1,r]
    build(u*2,l,mid);	//递归构造左儿子结点
    build(u*2+1,mid+1,r);//递归构造右儿子结点
    //一般build后面都要跟着pushup，具体要看题意
    pushup(u);//更新父节点 从下往上传递信息
}

2.单点修改

在线段树中，根节点(编号为1的节点)是执行各种指令的入口。

我们需要从根节点出发，递归找到代表区间[x,x]的叶子节点，然后从下往上更新[x,x]以及它的所有祖先节点上保存的数据信息。

//更新函数，这里是实现最大值 ，同理可以变成，最小值，区间和等
void pushup(int u)
{
    tr[u].val=max(tr[u*2].val,tr[u*2+1].val);
}
//递归方式更新  
void modify(int u,int x,int v)	//u是当前节点，x是我们想要修改的节点的下标，v是修改的值
{
    //左端点等于右端点，即为叶子结点，直接修改为v即可
    if(tr[u].l==tr[u].r)
    {
        tr[u].val=v;
        return;	//回溯
    }
    //mid则为中间点，左儿子的结点区间为[l,mid],右儿子的结点区间为[mid+1,r]
    int mid=(tr[u].l+tr[u].r)/2;
    //如果需要更新的结点x在左子树区间
    if(x<=mid)
        modify(u*2,x,v);
    //如果需要更新的结点在右子树区间
    else
        modify(u*2,x,v);
    //从下往上更新信息
    pushup(u);
}

3.区间查询

区间查询时一条形如"Q l r"的指令，例如查询序列A在区间[L,R]上的最大值，即m a x L ≤ i ≤ R ( A [ i ] ) max_L\leq i\leq R(A[i])max
L

≤i≤R(A[i])。我们只需要从根节点出发，递归执行以下过程：

若待查询区间[L,R]已经完全覆盖了当前节点所代表的区间，即当前树中的这个节点所代表的区间[t r [ u ] . l tr[u].ltr[u].l，t r [ u ] . r tr[u].rtr[u].r] ⊆ [ L ， R ] \subseteq [L，R]⊆[L，R]，则立即回溯，并且该节点的val值为候选答案。
若左子节点所代表的区间与待查询区间[L,R]有重叠部分，则递归访问左子节点。
若右子节点所代表的区间与待查询区间[L,R]有重叠部分，则递归访问右子节点。

递归方式区间查询区间[L,R]
int query(int u,int L,int R)//[L,R]即为要查询的区间,u是当前节点

{
    //如果当前结点的区间真包含于要查询的区间内，则返回结点信息且不需要往下递归
    if(L<=tr[u].l&&tr[u].r<=R)
        return tr[u].val;
    int ans=-INF;	//返回值变量，根据具体线段树查询的什么而自定义
    int mid=(tr[u].l+tr[u].r)/2; //mid则为中间点，左儿子的结点区间为[l,mid],右儿子的结点区间为[mid+1,r]
    //如果左子树和需要查询的区间交集非空，即左子节点和需要查询的区间有重叠
    if(L<=mid)
        ans=max(ans,query(u*2,L,R));
     //如果右子树和需要查询的区间交集非空，即右子节点和需要查询的区间有重叠
    if(r>mid)
        ans=max(ans,query(u*2+1,L,R));
    return res;	 //返回当前结点得到的信息
}

4.*区间修改

为此引入线段树的延迟标记概念，也叫 lazy tag，这个标记一般用于处理线段树的区间更新。

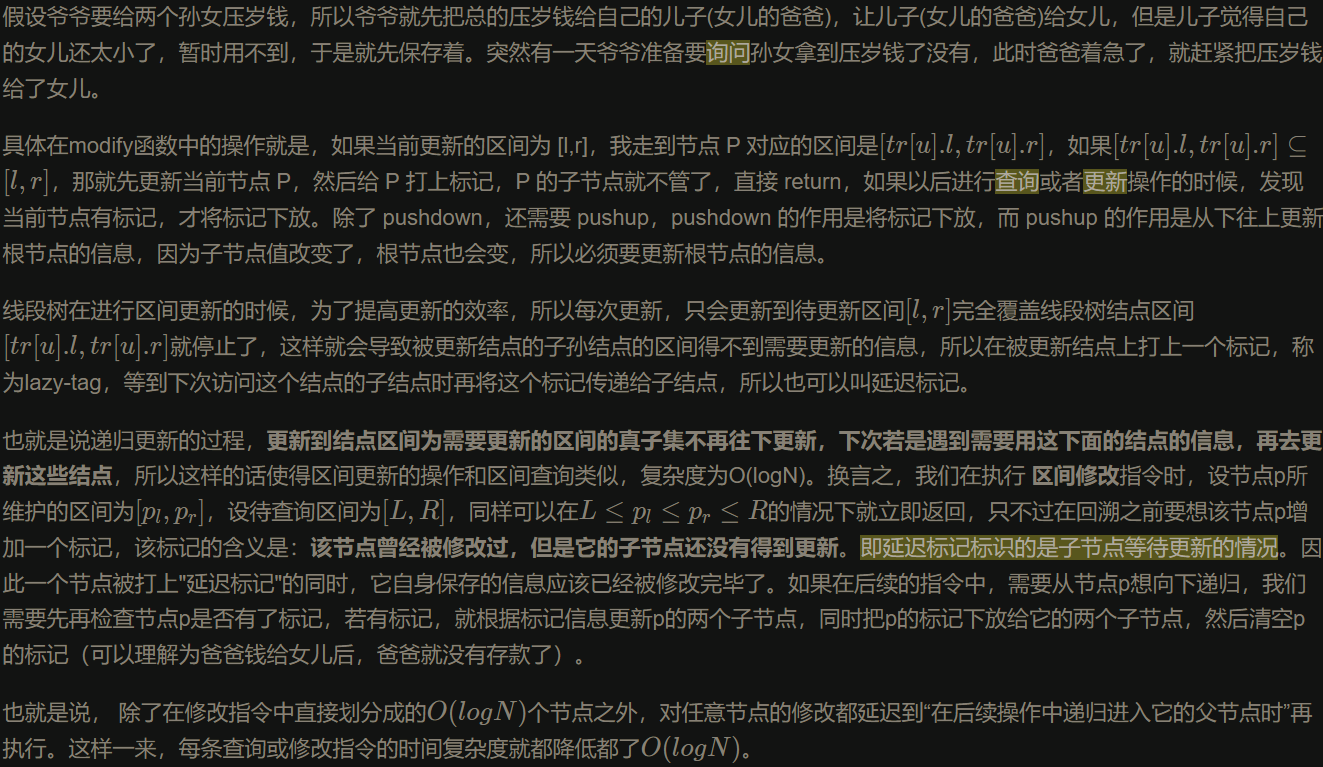
延迟标记：节点结构体中新增一个标记，记录这个节点是否会进行某种修改，对于任意区间的修改，我们先按照区间查询的方式将其划分成线段树中的节点，然后修改这些节点的信息，并给这些节点打上标记。在修改和查询的时候，如果我们到了一个节点 P，并且要继续查看其子节点，那么我们就要看看节点 P 是否被标记，如果有，则需要按照其标记首先修改子节点的信息，并且给子节点都打上相同的标记，同时取消节点 P 的标记，这一操作称为标记下放，也叫 pushdown。举个栗子：

struct NOde{
    int l,r;
    int val;
    int tag;
}tr[4*N];
//父节点把标记下放给左右节点
void pushdown(int u)
{
    Node &root=tr[u],&left,&right;	//root是父节点，left是左子节点，right是右子节点
    //如果父节点有标记	（可以理解爷爷把给孙女的压岁钱，给爸爸先存放了）
    if(root.tag!=0)
    {
        left.tag+=root.tag;//更新左子树的tag值  即爸爸把压岁钱下放给了女儿
        right.tag+=root.tag;//更新右子树的tag值  即爸爸把压岁钱下放给了女儿
        left.val+=root.tag;//左子树的最值加上tag值	即女儿的压岁钱又多了，多的这部分压岁钱来源于父亲给的tag
        right.val+=root.tag;//右子树的最值加上tag值	即女儿的压岁钱又多了，多的这部分压岁钱来源于父亲给的tag
        root.tag=0;	//爸爸把钱给女儿后，自己就没有存款了
    }
}
//递归更新区间 u是父节点，更新区间为[L,R]，更新值为v
void modify(int u,int L,int R,int v)
{
    //如果当前结点的区间真包含于要更新的区间内
    if(L<=tr[u].l&&tr[u].r<=R)
    {
        tr[u].tag+=v;		//给当前u节点打上标记
        tr[u].val+=v;		//最大值加上v之后，此区间的最大值也肯定是加v
        return;
    }
    //重难点，查询tag标记，更新子树
    pushdown(u);	//下放延迟标记
    int mid=(tr[u].l+tr[u].r)2;
    //如果左子树和需要更新的区间交集非空
    if(L<=mid)
        modify(u*2,L,R,v);
    //如果右子树和需要更新的区间交集非空
    if(R>mid)
        modify(u*2+1,L,R,v);
    //更新父节点
    pushup(u);
}
//递归方式区间查询
int query(int u,int L,int R)
{
    if(L<=tr[u].l&&tr[u].r<=R)
        return tr[u];
    //爷爷开始来询问爸爸有没有把钱给女儿了，那么爸爸才想起来，所以爸爸要把钱给女儿了
    pushdown(u);/**每次都需要更新子树的tag标记*/
    int res = -INF;    //返回值变量，根据具体线段树查询的什么而自定义
    //mid则为中间点，左儿子的结点区间为[l,mid],右儿子的结点区间为[mid+1,r]
    int mid=(tr[u].l+tr[u].r)/2;
    //如果左子树和需要查询的区间交集非空,说明有部分信息在左子树中，递归查询左孩子区间
    if(L<=mid)
        res=max(res,query(u*2,L,R));
    //如果右子树和需要查询的区间交集非空，说明有部分信息在右子树中，递归查询右孩子区间
    if(R>mid)
        res=max(res,query(u*2+1,L,R));
    return res;//返回当前结点得到的信息
}

注意看pushdown这个函数，也就是当需要查询某个结点的子树时，需要用到这个函数，函数功能就是更新子树的tag值，可以理解为平时先把事情放着，等到哪天要检查的时候，就临时再去做，而且做也不是一次性做完，检查哪一部分它就只做这一部分。值得注意的是，使用了Lazy_tag后，我们再进行区间查询也需要改变。

5.*注意点

"区间内的最大值"和"区间的累加和"的query函数形式是一样的，设为A；"区间内的最大公约数"和"最大连续子段和"的qeury函数形式是一样的，设为B。但是A和B的形式有所不同

对于A类，与B类的不同点

int query(int u,int L,int R)
{
    //此处省略
    //
    //
    int mid=(tr[u].l+tr[u].r)/2;
    if(L<=mid)//如果左子树和需要查询的区间交集非空,说明有部分信息在左子树中，递归查询左孩子区间
        //递归进入左子树  
    if(R>mid)//如果右子树和需要查询的区间交集非空，说明有部分信息在右子树中，递归查询右孩子区间
        //递归进入右子树
}

对于B类，与A类的不同点

Node query(int u,int L,int R)
{
     //此处省略
    //
    //
    int mid=(tr[u].l+tr[u].r)/2;
     //如果待查询区间完全在节点所维护区间的左区间
    if(R<=mid)
        return query(u*2,L,R);
     //如果待查询区间完全在节点所维护区间的右区间
    else if(L>mid)
        return query(u*2+1,L,R);
     //如果待查询区间横跨在节点所维护区间的左右区间
    else
    {
        	Node left=query(u*2,L,R);   //左子节点
            Node right=query(u*2+1,L,R);    //右子节点
            Node res;   //res是left和right的父节点
            pushup(res,left,right);
            return res;
    }
}

单点修改函数和区间修改函数也是有不同点的：

单点修改函数：

void modify(int u,int x,int v)
{
    if(tr[u].l==x&&tr[u].r==x)
    {
        //此处省略
        return;
    }
    int mid=(tr[u].l+tr[u].r)/2;
    if(x<=mid)
        modify(u*2,x,v);
    else
        modfify(u*2+1,x,v);
    pushup(u);
}

区间修改函数

void modify(int u,int L,int R,int v)
{
    if(L<=tr[u].l&&tr[u].r<=R)
    {
        //此处省略；
        return;
    }
    pushdown(u);
    int mid=(tr[u].l+tr[u].r)/2;
    if(L<=mid)
        modify(u*2,L,R,v);
    if(R>mid)
        modify(u*2+1,L,R,v);
    pushup(u);
}

RMQ

RMQ（Range Minimum/Maximum Query），即区间最值查询，是指这样一个问题：对于长度为n的数列A，回答若干次询问RMQ(i,j)，返回数列A中下标在区间[i,j]中的最小/大值。

本文介绍一种比较高效的ST算法解决这个问题。ST（Sparse Table）算法可以在O(nlogn)时间内进行预处理，然后在O(1)时间内回答每个查询。

1.预处理

设A[i]是要求区间最值的数列，F[i, j]表示从第i个数起连续2^j个数中的最大值。（DP的状态）

例如：

A数列为：3 2 4 5 6 8 1 2 9 7

F[1，0]表示第1个数起，长度为2^0=1的最大值，其实就是3这个数。同理 F[1,1] = max(3,2) = 3, F[1，2]=max(3,2,4,5) = 5，F[1，3] = max(3,2,4,5,6,8,1,2) = 8;

并且我们可以容易的看出F[i,0]就等于A[i]。（DP的初始值）

我们把F[i，j]平均分成两段（因为F[i，j]一定是偶数个数字），从 i 到i + 2 ^ (j - 1) - 1为一段，i + 2 ^ (j - 1)到i + 2 ^ j - 1为一段(长度都为2 ^ (j - 1))。于是我们得到了状态转移方程F[i, j]=max（F[i，j-1], F[i + 2^(j-1)，j-1]）。

2.查询

假如我们需要查询的区间为(i,j)，那么我们需要找到覆盖这个闭区间(左边界取i，右边界取j)的最小幂（可以重复，比如查询1，2，3，4，5，我们可以查询1234和2345）。

因为这个区间的长度为j - i + 1,所以我们可以取k=log2( j - i + 1)，则有：RMQ(i, j)=max{F[i , k], F[ j - 2 ^ k + 1, k]}。

举例说明，要求区间[1，5]的最大值，k = log2（5 - 1 + 1）= 2，即求max(F[1, 2]，F[5 - 2 ^ 2 + 1, 2])=max(F[1, 2]，F[2, 2])；

void ST(int n) {//预处理dp
    for (int i = 1; i <= n; i++)//2^0 = 1 
        dp[i][0] = A[i];
    for (int j = 1; (1 << j) <= n; j++) {//指数从1到区间内最小 
        for (int i = 1; i + (1 << j) - 1 <= n; i++) {//右边界不超出n 注意要-1
            dp[i][j] = max(dp[i][j - 1], dp[i + (1 << (j - 1))][j - 1]);//递归 两个子区间内最大值
        }
    }
}
int RMQ(int l, int r) {//查询
    int k = 0;
    while ((1 << (k + 1)) <= r - l + 1) k++;//取得包含区间的最小指数
    return max(dp[l][k], dp[r - (1 << k) + 1][k]);
}

差分

一维差分

#include <iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N],b[N];//a为原数组，b为差分数组
int n,m;
 
void insert(int l,int r,int c)//要想在使原数组[l,r]区间的数全加c,就得在差分数组b[l]+=c、b[r+1]-=c,最后求前缀和即可
{
    b[l] += c;
    b[r + 1] -= c;
}
int main ()
{
    scanf ("%d%d",&n,&m);
    for (int i = 1;i <= n;i++) scanf ("%d",&a[i]);
    for (int i = 1;i <= n;i++) insert(i,i,a[i]); //初始化差分数组b[n]
    while (m--)
    {
        int l,r,c;
        scanf ("%d%d%d",&l,&r,&c);
        insert(l,r,c);
    }
    for (int i = 1;i <= n;i++) b[i] += b[i - 1];
    for (int i = 1;i <= n;i++) printf ("%d ",b[i]);
    return 0;
}

二维差分

#include <iostream>
using namespace std;
const int N = 1010;
int a[N][N],b[N][N];
int n,m,q;
void insert(int x1,int y1,int x2,int y2,int c)
{
    b[x1][y1] += c;	
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}
int main ()
{
    scanf ("%d%d%d",&n,&m,&q);
    for (int i = 1;i <= n;i++)
        for (int j = 1;j <= m;j++)
            scanf ("%d",&a[i][j]);
    for (int i = 1;i <= n;i++)
        for (int j = 1;j <= m;j++)
            insert(i,j,i,j,a[i][j]);//初始化
    while (q--)
    {
        int x1,y1,x2,y2,c;
        scanf ("%d%d%d%d%d",&x1,&y1,&x2,&y2,&c);
        insert(x1,y1,x2,y2,c);
    }
    for (int i = 1;i <= n;i++)
        for (int j = 1;j <= m;j++)
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];//二维前缀和
    for (int i = 1;i <= n;i++)
    {
        for (int j = 1;j <= m;j++)
        {
            printf ("%d ",b[i][j]);
        }
        printf ("\n");
    }
    return 0;
}